소개: 아래는 [Science/사이언스] 지에 실린 최신 음악학 논문을 root2a님께서 번역한 것입니다. ㅡ kguitar


* 음악적 공간 탐구
- Julian Hook

Science  VOL 313 7 July 2006


악보는 수직축이 음고를, 수평축이 시간을 나타내는 그래프이다. 이런 명백한 단순성과, 피타고라스 시대 이래로 많은 음악적 현상 근저에 수학적 법칙들이 있다는 인식에도 불구하고, 음악적 현상들이 작용하는 공간의 수학적 구조에 대한 이해가 여전히 단편적이라는 사실이 놀라울 지도 모른다. 그러나 Tymoczko가 72쪽에서 보인 것처럼 (1), 음고 영역조차도 처음 보기 보다는 훨씬 더 복잡하다.

단순히 어떤 음고 구조들(pitch structures)이 적당하고 또 언제 두 음고를 “같다”고 여겨야 하는지 단순히 결정하는 것은 어려울 수 있다. 두 개의 다른 ‘C 처럼, 같은 이름이지만 옥타브가 다른 음들은 같다고 여겨져야 하는가? C# 이나 Db 처럼, 이명동음들은 어떤가? (이 둘은 피아노에서 하나의 음이지만 종종 아주 다른 음악적 용도로 쓰인다.) 더구나 화성적 구조들은 낱낱의 음들이 아니라 화음들이다. 만약 화음을 구성하고 있는 성부 중 두 음을 서로 바꾸었을 때, 그 코드는 그 전 코드와 같은 코드인가? C 두 개를 갖고 있는 4음 화음은 C 하나를 갖고 있는 3음화음으로 줄여야 하는가? 악기 조율은 중요한가?

음악적 감성은 음악의 맥락과 분석 목표에 따라 이들 질문에 다른 답을 줄 것이다. 음악 이론가들은 화음들을 장3화음들과, 어떤 적절한 공간에서 평행이동 (음악적 용어로 이도(transposition))과 때로는 반사 (전위(inversion))로 묶여진 군(群)화음들과 같은 카테고리로 분류한다. 서양 음악가들은 피아노에서 연주 될 수 있는 반음계에 해당하는 음고공간의 이산성에 익숙해져 있지만, 일반적인 문제에서는 연속적인 음고 변화가 가능한 더 큰 공간을 고려해야 한다. 몫공간들 (같은 점들을 “함께 붙여“ 얻은)과 그 위에 작용하는 군(群) 구조의 모임이 다양한 등치관계들로 인해 만들어 진다.  이곳에 발표된 Tymoczkos 연구는 이들 공간에 대한 고도로 일반화된 특징을 나타내고 공간들의 기하와 그 공간속에 있는 화음들의 음악적 행동을 연관 짓는 야심찬 프로젝트의 일부분이다 (2).

수학적 음악이론은, 현직 음악가들이나 심지어 많은 전문 음악이론가들에게 조차 미지의 영역임에도 불구하고, 최근에 와서 크고 다양한 분야로 꽃피우고 있다. 화성적 요소들(harmonic materials)이 대부분의 이전 음악보다 훨씬 다양하고 복잡해진 20세기의 “탈 조성(post-tonal)" 음악의 등장으로 분석적 어려움이 제기 되었다. 음고류 집합이론 (3), 즉 이산적 12음 몫공간에 대한 연구는, 이러한 어려움에 대응하기 위한 수단으로 발전되었다. 온음계적 집합이론 (4,5)은 12음 반음계와 한 옥타브에 7개의 비균할 음들이 있는 C 장음계 같은 온음계 (많은 음악양식에서 크게 중요한 음계의 종류임) 사이의 미묘하고 아름다운 관계를 연구하고 있다. 음계론 (6,7)은 반음계와 온음계의 음 개수들(chromatic and diatonic cardinalities)에 변화를 허용하며, 또 때때로 조율과 음향학과 더불어 음계의 구조적 성질과 그 하위음계를 좀 더 넓게 연구하고 있다.

지난 20년간 음악적 공간위에 작용하는 변환군(群)들은 다양한 조건에서 지극히 유용한 모델들임이 증명되어 왔다. 변환은 화음들 (혹은 다른 음악적인 것) 사이의 관계들을 기술하는 수학적 함수들이다; 종종 이들은 대수적 군(群)을 이루고 음정의 음악적 개념들과 밀접한 관계를 갖고 있다 (8).

특히 활발한 분야는 신(新)리만이론(Neo-Riemannian theory)이다. 이 이론에서는 현대적 군(群)이론의 테크닉과 독일 음악학자 Hugo Riemann (1849-1919)및 그의 동시대인들의 연구에서 비롯된 영감을 통합 하고 있다. 그 기본적인 형태에서 (9, 10), 신(新)리만이론은 열 두 개의 장화음과 12개의 단화음사이의 어떤 변환적 관계를 연구한다. 이는 대수적으로 우아하고, 음악적으로 시사점이 많으며, 또 Tonnetz (tone network)라고 알려진 다양한 형태의 그래프들-작곡은 이 안에서 화성 경로(harmonic path)를 따르게 된다-로 쉽게 시각화 시킬 수 있는 방법들로 구현된다  (그림 참조).






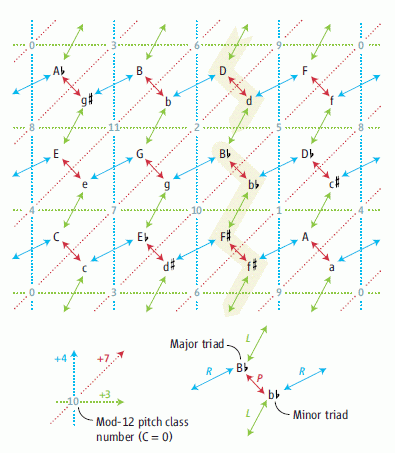
이 그림에서 점선으로 표시된 배경 그래프에 있는 12진법의 수들은 C=0부터 B=11까지의 음고류들을 나타낸다 (옥타브 등치성을 고려한 음고들). 이들은 음악적으로 중요한 음정들로 배열되어 있다: 대각선(붉은선)으로 완전 5도(음정 7), 수직(파란선)으로 장 3도(음정 4), 그리고 수평(초록선)으로 단 3도(음정 3) 이다. 이 2차원 그래프는 오른쪽 경계와 왼쪽 경계를 위쪽과 아래쪽 경계를 붙이기 전 토러스이다. 실선 화살표로 표시된 전경 그래프는, 대응되는 배경 음고류들로 만들어지는 삼각형의 내부에 위치한 장/단 3화음들(각각 대문자와 소문자로 나타난)을 나타낸다: 예를 들면, Bb 장3화음은 Bb음(음고류 10), D음(음고류 2), 그리고 F음(음고류 5)으로 이루어져 있다. 각각의 3화음은 P(Parallel, 붉은색 화살표), R(Relative, 파란색), 그리고 L[Leitton-wechsel (이끔음 교환, leading tone exchange), 초록색] 변환들로 얻어지는 반대 조성의 세 개의 서로 다른 3화음들과 음 두 개가 같다. 이 변환들은 12각형의 회전과 반사로 이루어지는 군(群)으로 order 24인 dihedral 군(群)과 동형(isomorphic)이다. 각각의 변환은 두 개의 음고류를 보존하고 작은 음정만큼 세 번째 음을 움직이는, 효율적인 성부진행을 나타내고 있다; 화살표들은 항상 같은 색의 점선들을 지난다. 베토벤의 화음진행은 (그래프에서 강조되고 그림의 아래쪽에 확대되어 있는), 토러스 위를 일주하는 Bb 장화음에서 시작하고 끝나는 PL-cycle이고, 또한 복합적인 PLPLPL 변환은 그 그룹의 항등원소임을 나타낸다.

Tonnetz는 음악적 공간에 대한 많은 가능한 기하적 표현들 중 하나일 뿐이다. 최근 연구는 신(新)리만방법을 더 크고 더욱 강력한 변환 그룹과, 3화음 외의 다른 종류의 화음들을 비롯한, 그리고 다양한 다른 방향들로 확장 시키고 있다 (12). 군(群)이론과 다른 대수적 테크닉과 더불어, 그래프이론, 조합이론, 기하 그리고 위상으로부터 나온 아이디어들이 음악에 적용되어 왔다. Tymoczko 등의 연구는, 화음공간에 대한 혁신적이고 광범위한 연구로서 이런 전략들을 포함하고 있다. 이 연구의 가장 매력적인 점 중 하나는 그 일반성이다: 본질적으로 Tonnetz나 음악적 관계에 대한 알려진 여러 다양한 서술들은 부분공간(subspace)이나 사영(projections), 그리고 단면(cross section)으로 나타나는 “모든 화음들의 공간“이 무엇인지 기술하려는 것을 목표로 한다. 여기에 나타나는 공간들은 특이점-기하적 구조가 국소적으로(locally) Euclidean이 아닌 점-들을 갖고 있으며 orbifold로 알려진 형태들이다 (더욱 고전적인 수학분야에서 최근의 위상 개념인 orbifold를 이용하려는 시도가 빈번해지고 있다). 그 밖의 다른 가치 있는 공헌에는 협화와 불협화, 공간들의 대칭성과 많은 음악적 관행사이의 연관성, 그리고  오랫동안 성공적인 작곡의 특징으로 인식되었던 화음대 화음 성부진행에 대한 여러 함의등과 같은 어려운 개념에 대한 새로운 관점이 포함된다.